I recently read this alarming report in Perspectives on Psychological Science (Kievit, 2011):

A group of international Bayesians was arrested today in the Rotterdam harbor. According to Dutch customs, they were attempting to smuggle over 1.5 million priors into the country, hidden between electronic equipment. The arrest represents the largest capture of priors in history.

“This is our biggest catch yet. Uniform priors, Gaussian priors, Dirichlet priors, even informative priors, it’s all here,” says customs officers Benjamin Roosken, responsible for the arrest. (…)

Sources suggest that the shipment of priors was going to be introduced into the Dutch scientific community by “white-washing” them. “They are getting very good at it. They found ghost-journals with fake articles, refer to the papers where the priors are allegedly based on empirical data, and before you know it, they’re out in the open. Of course, when you look up the reference, everything is long gone,” says Roosken.

This fake report is quite possibly the geekiest joke in the history of man, so you're forgiven if you don't get it right away. It's about statistics, so a very brief introduction is in order.

Psychologists typically investigate whether two groups (or one group under two conditions) differ from each other in some respect. For example, they may investigate whether men and women differ in their cleaning habits, by comparing the number of times that men and women vacuum each week. Here's some fake data for 6 participants (3 men and 3 women):

Men: 2, 2, 1 (Average = 1.67)
Women: 2, 3, 2 (Average = 2.33)

From this data you might conclude that women vacuum more often then men. But there are only 3 participants in each group and the difference isn't really that big. So could this apparent difference be a coincidence? Perhaps, by chance, we selected an exceptionally sloppy guy (1x) and an exceptionally proper girl (3x).

In order to find out, we do some calculations. And we come up with a number that tells us something about how confident we should be that the observed difference is real (i.e., generalizes to the population). This number is called a p-value and, in this case, it is .18.

So what does a p-value of .18 mean? Here it comes: It means that, assuming that there is really no difference between men and women, and assuming that we tested precisely as many participants as we planned beforehand and never had any intention of doing otherwise, the chance of finding a difference as large as we did, or larger, is .18. Right. The threshold that is typically used is .05. So, because lower p-values are “better”, we conclude that our p-value of .18 does not allow us to draw any conclusions. We cannot even conclude that there is no difference. Maybe, maybe not.

In practice, we interpret the p-value as measuring the evidence for the “alternative” hypothesis, which is the hypothesis that the observed difference is real. So, in our example, the alternative hypothesis is that men and women are not equally clean (or sloppy). Typically, the alternative hypothesis is what a researcher wants to prove. I suppose that, in an indirect way, evidence for the alternative hypothesis is what the p-value measures. But p-values are subtle creatures and hard to interpret correctly (if you don't agree, please re-read the italicized sentence above).

There is another big problem with p-values. They depend on the subjective intentions of the researcher. And subjectiveness is rarely a good thing in science. Specifically, the researcher must not allow himself to analyze the data twice, or more importantly, not give himself the possibility of stopping the experiment at two different points in time. Because if he does, there are two opportunities for a false alarm (i.e., concluding that a difference is real, when it's really not), whereas the p-value assumes that there was only one opportunity. This matters, and if you do check twice, you need to take this into account by adjusting your p-value.

Are you still with me? If so, let's consider the following paradoxical situation (and if not, the following example may help clarify things). Let's assume that researchers Bob and Harry are collaborators on a project and have tested 50 subjects. Their aim was to compare condition A to condition B, and conditions were varied "within-subjects" (i.e., all participants performed in both conditions). They analyzed the data separately (for some reason, perhaps they don't communicate that well). Harry, the proper one, only looked at the data after the planned 50 subjects and concludes that there is a significant difference between A and B, with a p-value of .049 (smaller than .05, so score!). But Bob, the impatient one, decided to look at the data already after 25 subjects, without telling Harry. He felt that if there was a clear difference after 25 subjects, they should stop the experiment to save time and money. But there wasn't, so the full 50 subjects were tested anyway. Bob now has to compensate for the fact that he looked at the data twice. Therefore, with the exact same data as Harry, he arrives at a p-value of .10 (larger than .05, so no luck). So Bob cannot draw any conclusion from the data. The same data that Harry is now submitting to Nature. If only Bob hadn't taken that extra peek!

Clearly, this way of doing statistics is weird. It gives a counterintuitive statistical measure, the p-value, which is notoriously hard to interpret. And worse, it mixes the intentions of the researcher with the strength of the data. So can we do better?

Luckily, according to some statistical experts we can. With Bayesian statistics. I won't attempt to explain how it works in detail, because I have only the faintest clue myself. But it sounds beautiful! In the May issue of Perspectives on Psychological Science there are some very good (and surprisingly entertaining) papers on the subject (Dienes, 2011; Kruschke, 2011; Wetzels et al., 2011; see also Wagenmakers, 2007).

As I understand it, the idea is that you have two hypotheses (A and B) that you want to pit against each other. For example, hypothesis A could be that there is no difference between two groups, which would be the default “null” hypothesis in classical statistics. Hypothesis B could be that there is a difference, which would be the alternative hypothesis in classical statistics. But you can have more complex hypotheses as well, taking into account your predictions in more detail (exactly what kind of difference do you expect?). Next, you assign a probability to both hypotheses: How likely do you think each of the hypotheses is before you have even begun to collect data? These are the priors which have been allegedly smuggled into Holland. If you have no clue, or if you don't want to seem biased, you simply give these priors some default value.

Next, you update these probabilities with each data-point that you collect, using Bayes theorem. For example, if hypotheses A and B were initially equally likely to be true, but a new data-point favors A, you decide that now A is slightly more likely. You collect data until you feel that there is sufficient evidence for one of the hypotheses. Note that the subjective intentions of the researcher are not a factor in this approach. And this is good, because as Dienes rhetorically asks: “Should you be worrying about what is murky [the intentions of the researcher] or, rather, about what really matters—whether the predictions really follow from a substantial theory in a clear simple way?”

I personally find it hard to understand why Bayesian statistics is not plagued by the same issues as classical statistics. I just can't seem to get my head wrapped around it. For example, one problem with p-values is that if you analyze your data after every participant (and don't correct for this), you will eventually always get a “significant” result. Supposedly, this is not the case with Bayesian statistics.

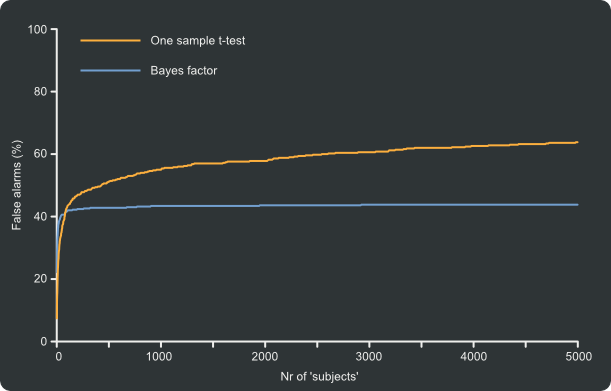
So I decided to run a simple test. I generated random “Subject data”, consisting of random values between -0.5 and 0.5. Obviously, in this case the null hypothesis is true, because the data does not, on average, deviate from 0. After every "subject" I calculated a Bayes factor (a Bayesian counterpart to the p-value) and a p-value. If the Bayes factor was larger than 3, a threshold which is supposedly comparable to the .05 p-value threshold, the “experiment” was considered to be a Bayesian false alarm. If the p-value was below .05 the “experiment” was considered to be a p-value false alarm. 500 “experiments” were simulated in this way. What is plotted on the y-axis of the graph below is the percentage of experiments in which a false alarm had occurred. What is plotted on the x-axis is how many subjects this took to happen.

And, indeed, using the p-value, the rate of false alarms is steadily increasing throughout the entire simulation (I stopped at subject 5000). Using the Bayes factor, the rate of false alarms tapers of rapidly. You get false alarms in the beginning, but collecting more data does not increase the number of false alarms. As you can see, there is generally speaking a huge number of false alarms: 40% using the Bayes factor and over 60% using the p-value. Clearly, I was a little trigger-happy in this simulation.

At any rate, don't take my little simulation too seriously. But I would encourage anyone who ever deals with statistics to read some of papers listed below. They really are a breath of fresh air.

Resources

A convenient online tool for calculating a Bayes factor: http://www.lifesci.sussex.ac.uk/home/Zoltan_Dienes/inference/bayes_factor.swf

The Python script used for the simulation: bayesian_radicals.py

Doing Bayesian data analysis workshops

References