We all know shortcuts like this:

Photo: Jan-Dirk van der Burg (olifantenpaadjes.nl)
Trails of this sort go by various names. In a photo album devoted entirely to the subject, the Dutch photographer Jan-Dirk van der Burg has coined (or at least popularized) the term "elephant trail" (olifantenpaadje). Wikipedia adopts the more sensuous "desire path". And, of course, there is the simple "shortcut". But regardless the name, it is an intriguing phenomenon. Because these trails are shortcuts, to be sure, but usually not quite the shortest path.

Photo: Jan-Dirk van der Burg (olifantenpaadjes.nl)
But why? If you're going to leave the sidewalk anyway, why not head straight to wherever you need to go? Why the little curve, the minor inefficiency? Surely not to please the likes of van der Burg, who revel in their shape and form.

Photo: Jan-Dirk van der Burg (olifantenpaadjes.nl)
Surprisingly enough, desire paths can be modeled fairly easily. Helding and colleagues have proposed a model in which they are the result of only two opposing "social forces": The tendency to take the shortest path (i.e., a straight line) and the tendency to take the most comfortable path.
The crux of the model is the assumption that paths become increasingly more comfortable as people use them. Which is true, of course, because usage smoothens a path by killing off vegetation, etc. Another factor is the social comfort of walking where others have walked before: Most people do not want to be a rogue wanderer. Therefore, to use the technical term, desire paths are autocatalytic: Usage makes a path more comfortable, which, in turn, leads to more usage.
This explains the emergence of clear, well defined paths, where you might expect a jumble. But why don't these paths go in straight lines? Well, according to the model, they do at first. Let's assume that a field of grass is initially entirely uniform, so that any part of the grass is as comfortable to walk on as any other part. In that situation, paths are determined solely by the tendency to take the shortest route, so people start off by walking in straight lines.
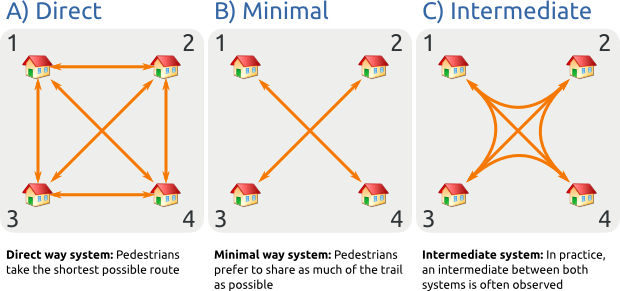
However, the situation changes as soon as paths begin to emerge. Let's assume that three paths leave house 1, going to houses 2, 3, and 4. Initially, these paths will go straight as shown in (A) in the figure above. Therefore, there are three distinct paths leading from 1 (and the same is true for the other houses, of course). These three paths are not used that much and thus, comfort-wise, they are only so-so. Next, what will happen is that the paths tend to merge. The reason for the tendency to merge is that this will decrease the combined length of all the paths, which consequently increases path-usage per length (assuming that the number of walkers stays the same), making the paths more comfortable to walk on. In it's extreme form, this will give rise to a minimal way system, as shown in (B).
In practice, however, people tend to compromise. Desire paths tend not to be the most direct route, but they rarely form a minimal way system either. Apparently, the conflicting goals of directness and comfort usually find their equilibrium in an intermediate form, as shown in (C). And one property of the intermediate form is that many of the paths are slightly curved.
So, quite possibly, that's how the desire path gets its little curve!
References
't Hart, M., & van der Burg, J. (2011). Olifantenpaadjes. Amsterdam, Netherlands: Burg Fotografie.
Helbing, D., Schweitzer, F., Keltsch, J., & Molnár, P. (1997). Active walker model for the formation of human and animal trail systems. Physical Review E, 56(3), 2527-2538. doi:10.1103/PhysRevE.56.2527 [Link: arXiv]